Math
Discover how math shapes the world around you! From using trigonometry to measure heights in construction, to understanding quadratics in physics, this course connects algebra and geometry to real-life problem-solving. Dive into hands-on activities and see how these concepts impact everyday life!
| Responsible | Andy Hakim |
|---|---|
| Last Update | 05/07/2025 |
| Completion Time | 2 days 3 hours 16 minutes |
| Members | 1 |
Grade 9
Academic
View all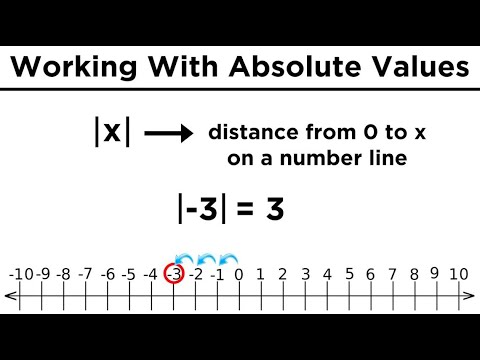
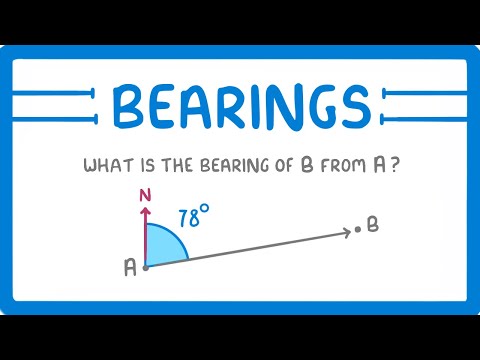
Intro to Absolute Values: Calculating, and Graphing
Preview
What are these funny little brackets? They represent absolute values. What's that? Well are you here to read this, or watch the clip? Let's go?
00:05
0
0

Quadratics Study Guide
Preview
Here is the ultimate study guide for anything and everything you need to know about quadratics. Go to jensenmath.ca for free math resources for all math topics. Hope you enjoy the video and that it helps your understanding.
Please consider subscribing. It really helps the channel.
0:00 - What is a Quadratic Relationship
2:09 - Standard Form
3:53 - Vertex Form
7:01 - Factored Form
9:33 - Factoring
12:18 - Solving by Factoring
14:37 - Solving by Completing the Square
16:17 - Quadratic formula
18:32 - The Discriminant
20:41 - 3 Ways to Find the Vertex
00:24
0
0
Extra
View all
The Discovery That Transformed Pi
Preview
How Newton Changed the Way We Calculate Pi
For millennia, mathematicians calculated π using geometry and slow convergence. Then Newton introduced a revolutionary approach using calculus, drastically accelerating the process.
References:
-
Books and Academic Sources:
- Arndt, J., & Haenel, C. (2001). Pi-Unleashed. Springer Science & Business Media. Link
- Dunham, W. (1990). Journey Through Genius: The Great Theorems of Mathematics. Wiley. Link
- Borwein, J. M. (2014). The Life of π: From Archimedes to ENIAC and Beyond. In From Alexandria, Through Baghdad (pp. 531–561). Springer. Link
Special Thanks:
- Alex Kontorovich – Professor of Mathematics at Rutgers University and Distinguished Visiting Professor for the Public Dissemination of Mathematics at the National Museum of Mathematics (MoMath)
Credits:
- Written by: Derek Muller & Alex Kontorovich
- Animation by: Ivy Tello
- Filming: Derek Muller & Raquel Nuno
- Edited by: Derek Muller
- Music: Jonny Hyman & Petr Lebedev
-
Additional Music: Epidemic Sound
- "Particle Emission"
- "Into the Forest"
- "Stavselet"
- "Face of the Earth"
- "Firefly in a Fairytale"
- Thumbnail by: Gianmarco Malandra & Karri Denise
00:19
0
0

How Imaginary Numbers Were Invented
Preview
How Giving Up Reality Solved the Cubic Equation
For centuries, a general solution to the cubic equation was considered impossible—until mathematicians embraced complex numbers, abandoning the strict requirement that math reflect physical reality.
References:
- Videos:
-
Books and Papers:
- Dunham, W. (1990). Journey Through Genius: The Great Theorems of Mathematics. Link
- Toscano, F. (2020). The Secret Formula, Princeton University Press. Link
- Bochner, S. (1963). The Significance of Some Basic Mathematical Conceptions for Physics, Isis, 54(2), 179–205. Link
- Muroi, K. (2019). Cubic Equations of Babylonian Mathematics, arXiv:1905.08034. Link
- Branson, W. (2014). Solving the Cubic with Cardano. Link
- Rothman, T. (2013). Cardano v Tartaglia: The Great Feud Goes Supernatural, arXiv:1308.2181. Link
- Siadat, M. V., & Tholen, A. (2021). Omar Khayyam: Geometric Algebra and Cubic Equations, Math Horizons, 28(1), 12–15. Link
- Merino, O. (2006). A Short History of Complex Numbers, University of Rhode Island. Link
-
Historical Works:
- Cardano, G. (1545). Ars Magna (Dover reprint, 1993). ISBN: 0-486-67811-3
- Bombelli, R. (1579). L’Algebra. Link
-
Software:
- Manim Community Developers. (2021). Manim – Mathematical Animation Framework (v0.13.1). Link
00:23
0
0

The SAT Question Everyone Got Wrong
Preview
How an SAT Question Became a Mathematical Paradox
A fascinating breakdown of an SAT question that led to widespread confusion and uncovered a deeper paradox in mathematics.
References:
- MindYourDecisions. Summary of this problem: YouTube
- Kyle Hill. More cool math about this problem: YouTube
- MinutePhysics. Discussion of a solar day: YouTube
- Murtagh, J. (2023). The SAT Problem That Everybody Got Wrong, Scientific American: Link
- United Press International (1982). Error Found in S.A.T. Question, New York Times: Link
- Yang (2020). Hardest SAT math problem?, Quora: Link
- Coin rotation paradox, Wikipedia: Link
- Simmons, B. (2015). Circle revolutions rolling around another circle, Math StackExchange: Link
- Sidereal time, Wikipedia: Link
- Solar Time vs. Sidereal Time, Las Cumbres Observatory: Link
- Zotti, G., et al. (2021). The Simulated Sky: Stellarium for Cultural Astronomy Research: Link
- Newspapers from 1980s–1990s, Newspapers.com: Link
- SAT Practice Test, College Board: Link
- Revolution Definition, NASA: Link
- Revolution Definition, Merriam-Webster: Link
- Earth motion animation, NASA: Link
- Satellite animation, NASA: Link
00:18
0
0